Redux da coloração de mapas
Esta seção reconsidera o problema de coloração do mapa da Seção 2.1. Desta vez, devemos representar as regiões adjacentes usando uma lista de regiões vizinhas, e não necessariamente armazenar o mapa explicitamente usando os dados do programa. Por exemplo, o mapa na Seção 2.1 poderia ser representado com a seguinte representação de lista de adjacência
[[1,2],[1,3],[1,4],[1,5],[2,3],[2,4],[3,4],[4,5]]A intenção é criar um programa para colorir o mapa que possa ser usado da seguinte forma:
?- color([[1,2],[1,3],[1,4],[1,5],[2,3],[2,4],[3,4],[4,5]],
[red,green,blue,yellow],Coloring).
Coloring = [[5,red],[4,green],[3,red],[1,blue],[2,yellow]] ; ... /* 48 solutions */Observe que aqui, por exemplo, 1 e 3 são adjacentes porque [1,3] pertence à lista, mas 3 é adjacente a 1 pelo mesmo motivo. Podemos calcular a relação de adjacência geralmente usando a seguinte definição.
adjacent(X,Y,Map) :- member([X,Y],Map) ; member([Y,X],Map).Observe a disjunção, ';', na cláusula. 'X' e 'Y' representam nomes de regiões e 'Map' é uma lista de adjacências. O predicado 'member' foi definido na última seção 2.7.
Observe ainda que uma lista de adjacências pode ser usada para definir o mapa, desde que cada região seja adjacente a pelo menos uma outra região (não regiões desconectadas). Portanto, pode-se calcular uma lista de nomes de regiões, dada a lista de adjacências. Aqui está uma definição do Prolog para isso.
find_regions([],R,R).
find_regions([[X,Y]|S], R,A) :-
(member(X,R) ->
(member(Y,R) -> find_regions(S,R,A) ; find_regions(S,[Y|R],A)) ;
(member(Y,R) -> find_regions(S,[X|R],A) ; find_regions(S,[X,Y|R],A) ) ).Esta é a forma de implicação do Prolog mais complicada até agora. Passe algum tempo entendendo o que ele diz antes de prosseguir. Por exemplo,
?- find_regions([[1,2],[1,3],[1,4],[1,5],[2,3],[2,4],[3,4],[4,5]],[],R).
R = [5,4,3,1,2]Preste atenção especial ao uso do parâmetro de acumulação (o segundo parâmetro).
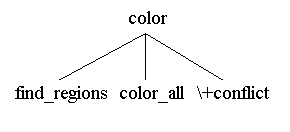
Agora, dada a lista de adjacências e uma lista de cores, deve-se ser capaz de calcular as cores adequadas -- ou seja, as cores em que as regiões adjacentes têm cores diferentes. Em outras palavras, afirmado de cima para baixo, a intenção é colorir o mapa calculando primeiro as regiões da lista de adjacências, depois colorir o mapa e depois verificar se a coloração não está em conflito. Retratado com uma árvore, temos
A árvore mostra a decomposição lógica de cima para baixo pretendida para o design do programa. Posteriormente, com os valores preenchidos para as variáveis, ela poderia se tornar uma árvore de cláusulas justificando alguma consequência particular do programa.
color(Map,Colors,Coloring) :-
find_regions(Map,[],Regions),
color_all(Regions,Colors,Coloring),
\+ conflict(Map,Coloring).
color_all([R|Rs],Colors,[[R,C]|A]) :-
member(C,Colors),
color_all(Rs,Colors,A).
color_all([],_,[]).
conflict(Map,Coloring) :-
member([R1,C],Coloring),
member([R2,C],Coloring),
adjacent(R1,R2,Map).É muito importante perceber onde o programa em execução faz as escolhas de coloração. Basicamente, isso acontece na primeira cláusula de definição de 'color_all', e as escolhas são determinadas por 'member'. Ao retroceder(backtracking) em 'member', escolhe-se outra cor.
Exercício 2.9 O programa é um tanto ineficiente porque espera até depois de ter colorido um mapa completamente antes de determinar se há um conflito na coloração. Modifique o programa para que suas cores e verificações contra conflito simultaneamente (antes de continuar a colorir mais regiões). Teste o programa modificado e o original em um mapa dos Estados Unidos.
Veja Também
- Código do Prolog para esta seção.
- 2.1 Coloração de mapas
- 2.7 Listas em Prolog
- 2.10 I/O Simples em Prolog
- Prolog Tutorial Sumário