Cut no Prolog
O predicado 'cut' do Prolog, ou '!', elimina escolhas em uma árvore de derivação do Prolog. Para ilustrar, primeiro considere um corte em um objetivo. Por exemplo, considere objetivo ?-p(X),!. para o programa P usado na seção 3.1.
Para a árvore de derivação anterior, isso significa que os ramos marcados com #2 e #3 são eliminados e, portanto, todas as sub-árvores abaixo dessas duas arestas também são cortadas. Então, isso corresponde apenas a produção da primeira resposta X=a:
?- p(X),!.
X=a ;
noAqui, tentamos fazer com que o Prolog encontrasse mais algumas respostas usando ';' mas elas já foram cortadas. Considere também:
?- r(X),!,s(Y).
X=a Y=a ;
X=a Y=b ;
X=a Y=c ;
noNote que que não há backtracking para esse primeiro objetivo. Além disso,
?- r(X), s(Y), !.
X=a Y=a ;
no...como esperado.
Suponha que ocorra um corte no corpo do programa. A regra de corte (acima) ainda se aplica quando o corte aparece como um sub-objetivo chamado. O corte é usado no corpo de uma determinada cláusula para evitar o uso de cláusulas que apareçam após a cláusula fornecida no programa. Para ilustrar, considere o seguinte programa:
part(a). part(b). part(c).
red(a). black(b).
color(P,red) :- red(P),!.
color(P,black) :- black(P),!.
color(P,unknown).A intenção é determinar uma cor para uma parte com base em informações específicas armazenadas, ou então concluir que a cor é 'desconhecida' de outra forma.
Uma árvore de derivação para o objetivo ?- color(a,C) é
... que corresponde com...
?- color(a,C).
C = red... e uma árvore de derivação para o objetivo ?- color(c,C). é...
... que corresponde com...
?- color(c,C).
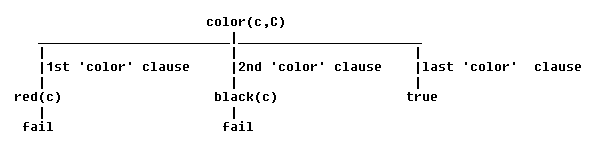
C = unknownO cut em Prolog é um dispositivo processual para controlar a satisfação do objetivo. O uso de 'cut' afeta os significados dos programas. Por exemplo, no programa 'color', a seguinte árvore de cláusulas do programa diz que 'color(a,unknown)' deve ser uma consequência do programa:
O corte no programa permite que Prolog "evite" esta resposta. Seria difícil modificar a definição da árvore de cláusulas do programa (para as consequências do programa) para refletir o significado procedimental do corte. No entanto, as árvores de cláusulas do programa ainda podem ser úteis para diagramar respostas que poderiam resultar sem o corte.
Exercício 3.2.1 (a) O que acontece se alguém usar o programa (suspeito):
max(X,Y,Y) :- Y>X, !.
max(X,Y,X).O que pode acontecer com o objetivo ?-max(1,2,1), por exemplo? Use uma árvore de cláusulas para mostrar que 'max(1,2,1)' é uma consequência do programa tal como está. Que suposição se deve fazer para que esta especificação do Prolog calcule corretamente o máximo de dois números?
Exercício 3.2.2 Suponha que, no programa P da seção 3.1, a cláusula #2 seja alterada para que leia:
p(X) :- q(X), !, r(X).Que respostas agora podem ser produzidas pela meta ?-p(X)? Por quê? Mostre por que usando a árvore de derivação Prolog (modificada para se adequar à nova regra).
O melhor uso do corte é como um dispositivo de eficiência, para evitar cálculos adicionais que não são desejados ou exigidos em um programa. O uso de um corte que apenas melhora a eficiência é conhecido como green cut. Um bom exemplo de green cut está na definição do predicado 'is_same-level_as' na seção 2.5. Caso contrário, o uso é um red cut. O uso do corte no programa 'color' é vermelho (trocadilho intencional), mas o corte foi usado para restringir as respostas, ou seja, bloquear o que de outra forma seria relatado como consequências do programa. Aqui está outra versão de 'color', usando a implicação de Prolog '->':
color(X,C) :- red(X) -> C = red
;
black(X) -> C = black
;
C = unknown.A próxima seção (3.3) pode ser adiada até ter lido as seções 2.13 e 2.14.